
We found locations such as (40,0,0) corresponds to the vortices formations as shown above. The plane locations were chosen by first finding an appropriate view of the vortices and then sliding the plane along the x-axis and identifying interesting features in the process. How did we choose the plane locations and what observations led to that decision. Part 1.4: Glyph Comparison: Cones, Cylinders, Arrows The four images below are rendered at location (40,0,0). However, we have also found the locations (30,0,0), (200,0,0), (300,0,0), (110,0,0) to be interesting and include renderings of these features as well. Among those we found the three locations (40,0,0), (70,0,0), (150,0,0) to be the most interesting. We tried positioning the plane in various locations. The color transfer function is used in the other visualizations as well. We also scale the glyphs by the magnitude. We use a cutting plane orthogonal to the x-axis and position it at three different locations. The first task is to visualize the velocity of the flow using glyphs (cones, cylinders, and arrows). Part 1: Glyphs for Visualizing the Vector Field Finally, we visualize the recirculation bubble by applying stream surfaces. In the next part, we apply isosurfacing along with streamlines in order to capture interesting properties.

We then visualize the flow using streamlines, stream tubes, and stream surfaces. In this work, we apply glyphs (cones, cylinders, and arrows) at three different locations to visualize the vector field. The flight configuration induces vortex breakdown where the symmetric vortices lose their simple structure and give rise to flow recirculation bubbles. The flow structures include primary, secondary, tertiary vortices (on each side of the wing). Stream = mesh.The task is to visualize the flow around the delta wing using the velocity (vector) information along with the lambda2 information. The result is a streamline of length 1, which confirms your observation. This example the cell length is 10 in each dimension, or sqrt(3)*10 on the diagonal, so when using max_time=1 with step_unit='cl' should result in a streamline generated using those parameters should either be 10 or sqrt(3)*10, depending on the exact implementation, in physical units. This is in contrast to the documentation, so it seems like a vtk bug to me. I have simplified your example and can confirm that it seems that vtk does not use ‘cell length’ for max time, it only uses ‘physical length’. Intel(R) oneAPI Math Kernel Library Version 2021.4-Product Build 20210904įor Intel(R) 64 architecture applications GPU Version : 4.6 (Core Profile) Mesa 21.3.6 GPU Renderer : Mesa Intel(R) HD Graphics 4600 (HSW GT2) This report helps us track down bugs and it is critical to addressing your bug: # Get system info
Paraview streamline code#
Please run the following code wherever you are experiencing the bug and paste the output below. Pyvista results using streamline parameters taken from Paraview test: Plotter.add_mesh(pyvista.Sphere(center=(-18,0,0), radius=0.3)) # just for reference Plotter.add_mesh(bfieldlines.tube(radius=0.01), color='r')

Max_steps=2000, # tried 20000, no difference
Paraview streamline zip#
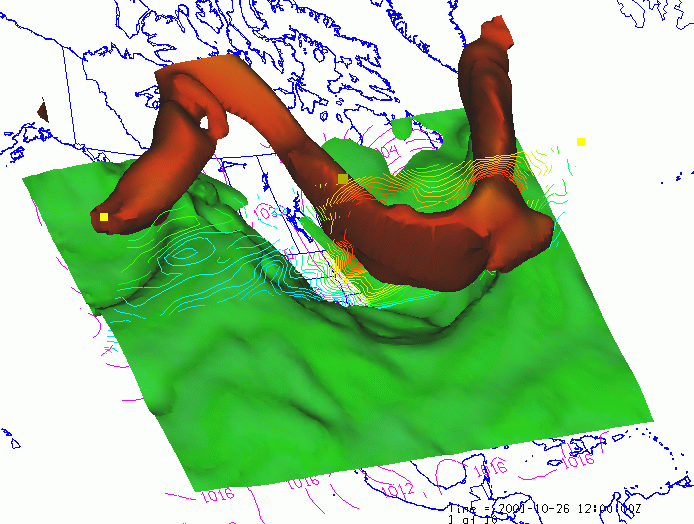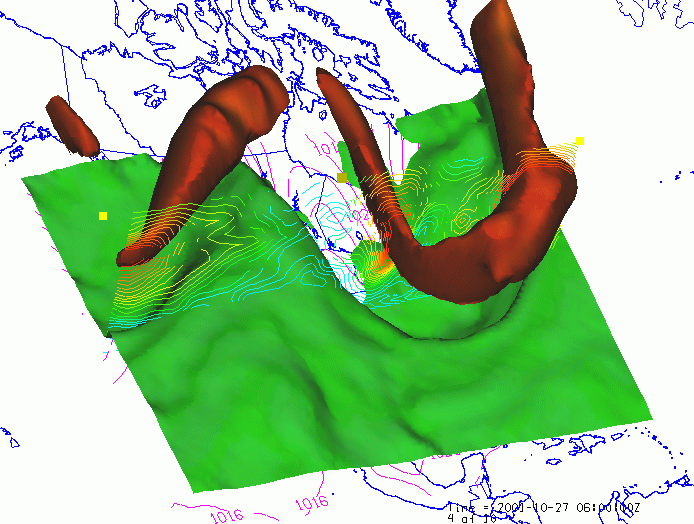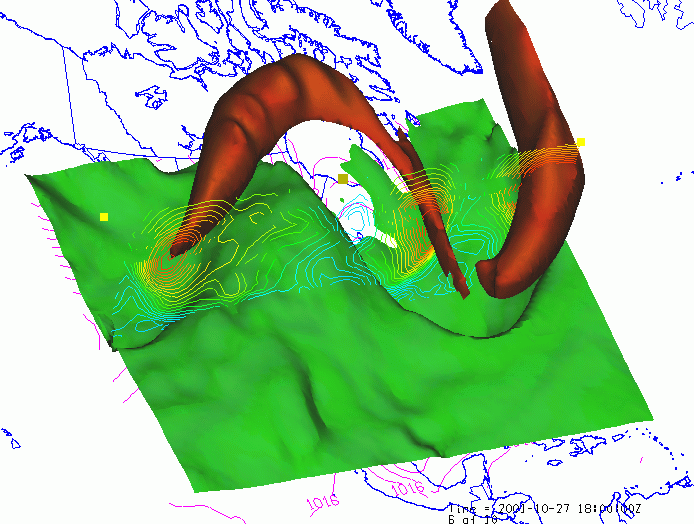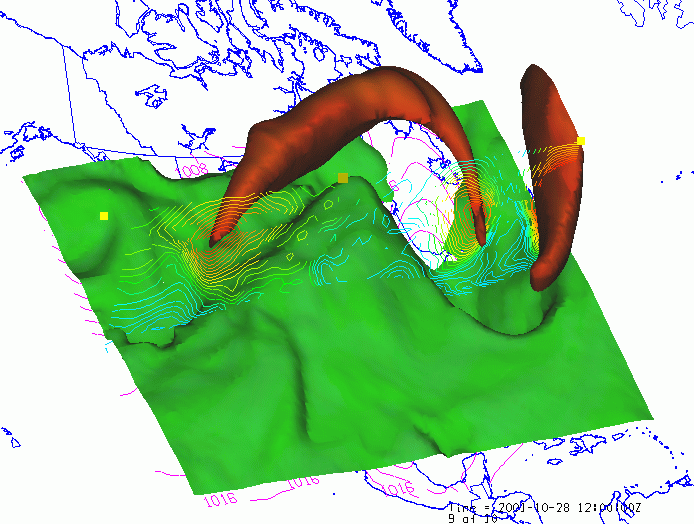
zip extension which was added to be recognized by github issue system): Input data (sorry for its nontrivial size ~ 10 MB please remove the. Please include a code snippet to reproduce the bug in the block below: I guess it could just be a parameter issue, but I haven’t found the cause. Streamlines using highly nonuniform vector field do not reproduce Paraview results. But still, the usage of the parameter MaximumPropagation might be improved, like I discussed in my own reply below.ĭescribe the bug, what’s wrong, and what you expect: Max_time = 4.0 * self.GetLength() / max_velocity Then, the default length figured out by the following code does not work well: if max_time is None: In my case, the magnitude of the vector field varies greatly. The default value max_time=None might not play well with certain data. After I set the max_time to 10, which is the default Maximum Streamline Length in Paraview, I can reproduce the Paraview results.


 0 kommentar(er)
0 kommentar(er)
